Literal equations are an important part of algebra, and they show up everywhere—from middle school math classes to science formulas used by professionals. At first glance, literal equations may look confusing, even intimidating. However, once you understand how they work, they become logical, useful, and surprisingly satisfying to solve.
This complete guide to literal equations is designed to help students, parents, and educators clearly understand what literal equations are, why they matter, and how to solve them step by step. With plain language, practical examples, and helpful strategies, this article builds confidence and skills that last.
By the end, you won’t just recognize literal equations—you’ll own them.
Understanding Literal Equations from the Ground Up
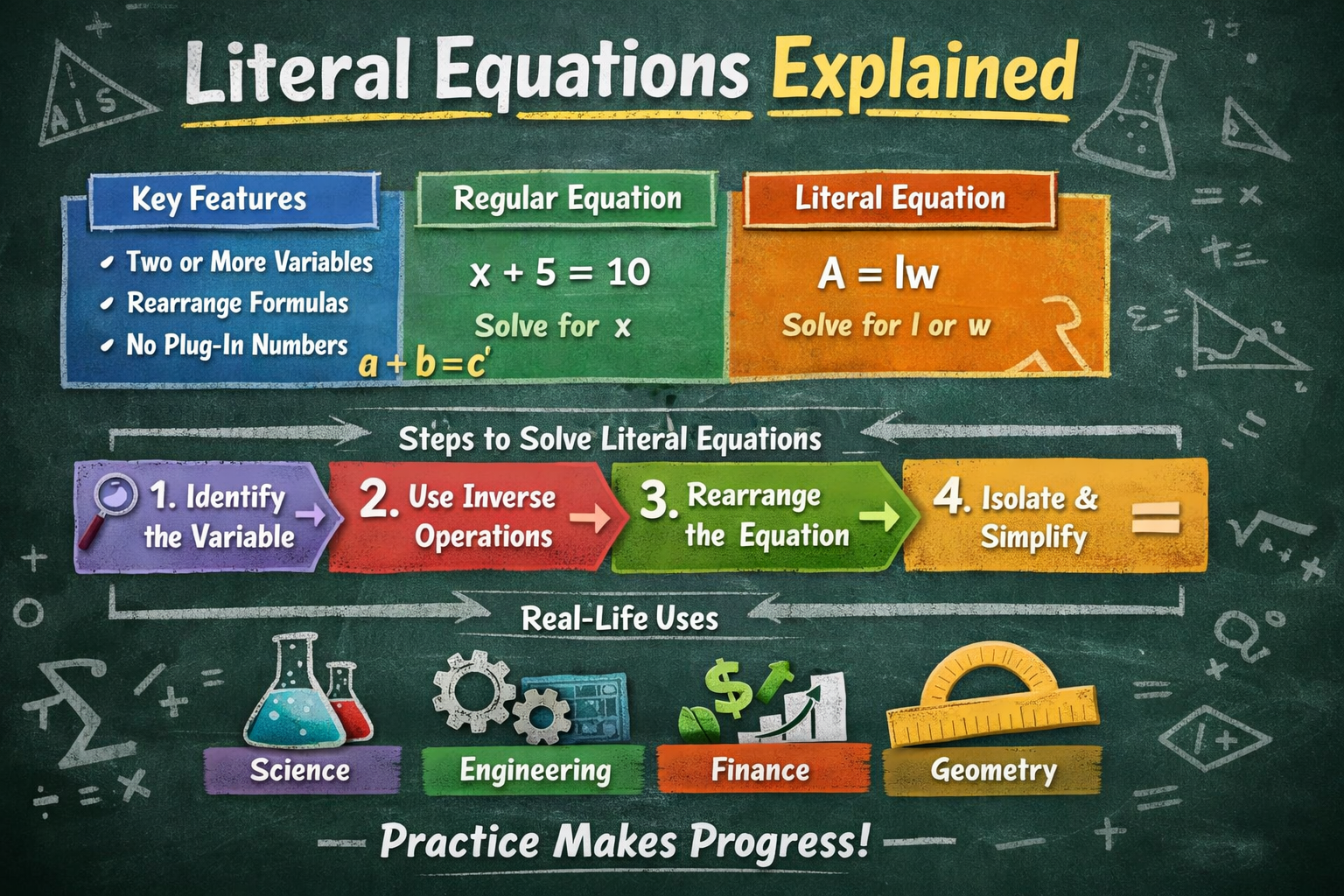
Literal equations are equations that contain two or more variables instead of just one. Unlike basic algebra equations that ask you to solve for a single unknown, literal equations ask you to rewrite the equation so one variable is isolated.
In simpler terms, you are rearranging the equation so that one letter stands alone on one side.
For example:
- A = lw
- F = ma
- V = IR
Each of these equations has more than one variable, which is exactly what makes them literal equations.
What’s important to remember is that you are not finding a number. Instead, you are changing the form of the equation. That small difference changes everything—and once you understand it, the rest falls into place.
Why Literal Equations Matter More Than You Think
You might be wondering why teachers spend so much time on literal equations. The reason is simple: they train your brain to think algebraically.
Literal equations appear in many real-life fields, such as:
- Science formulas
- Engineering calculations
- Economics models
- Geometry rules
- Computer programming logic
When you learn to work with literal equations, you’re learning how to rearrange information logically. That’s a skill that goes far beyond math class.
Even better, literal equations help students prepare for:
- Advanced algebra
- Physics
- Chemistry
- Standardized tests
- Problem-solving in real life
In short, mastering literal equations now saves time and frustration later.
Key Features That Define Literal Equations
Let’s break down what makes literal equations unique. Understanding these features helps you recognize them instantly.
Literal equations usually:
- Contain two or more variables
- Represent formulas or rules
- Require isolating a specific variable
- Use algebraic operations like addition, subtraction, multiplication, and division
They do not usually give you numbers to plug in. Instead, the goal is to rearrange the equation logically.
Think of it like rearranging furniture in a room. Everything stays inside the room, but the layout changes.
How Literal Equations Are Different from Regular Equations
This is a common point of confusion, so let’s clear it up.
Here’s a simple comparison:
| Regular Equation | Literal Equation |
|---|---|
| Has one variable | Has two or more variables |
| Solves for a number | Solves for a variable |
| Example: x + 5 = 10 | Example: A = lw |
| Answer is a value | Answer is a formula |
Once you spot multiple letters in an equation, you’re almost certainly dealing with a literal equation.
Step-by-Step Method to Solve Literal Equations
Solving literal equations isn’t about speed—it’s about strategy. Follow these steps, and you’ll stay on track every time.
Start by Identifying the Variable You Need
Before doing anything else, figure out which variable you are solving for. This keeps your work focused and prevents mistakes.
Ask yourself:
- Which letter needs to stand alone?
- What does the problem ask for?
Use Inverse Operations Carefully
Just like regular equations, literal equations rely on inverse operations. If a variable is multiplied, divide. If it’s added, subtract.
The goal is balance. Whatever you do to one side, you must do to the other.
Move Other Variables First
When multiple variables are involved, move everything except the variable you’re solving for.
For example:
- If a variable is added, subtract it first
- If it’s multiplied, divide last
Simplify and Check Your Work
Once the variable is isolated, simplify the equation if possible. Then, quickly check that your answer makes sense logically.
Common Examples of Literal Equations Explained Simply
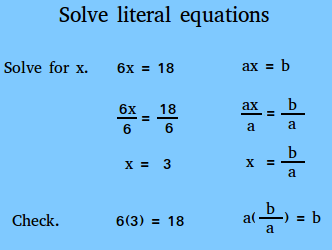
Let’s look at a few familiar formulas and see how literal equations work in action.
Area Formula
A = lw
If you want to solve for l, divide both sides by w:
l = A ÷ w
If you want to solve for w:
w = A ÷ l
Same equation—different focus. That’s the power of literal equations.
Speed Formula
d = rt
To solve for r, divide by t:
r = d ÷ t
To solve for t, divide by r:
t = d ÷ r
Once you understand the structure, the process becomes routine.
Mistakes Students Make with Literal Equations
Even strong students stumble when learning literal equations. The good news? Most mistakes are easy to fix once you know what to watch for.
Common errors include:
- Moving the wrong variable
- Forgetting to divide or multiply both sides
- Mixing up inverse operations
- Rushing through steps
- Skipping simplification
The best defense against these mistakes is slowing down and working step by step. Literal equations reward patience.
Smart Strategies to Master Literal Equations Faster
Want to improve quickly? These strategies help students build confidence and accuracy.
- Rewrite the equation neatly before starting
- Circle the variable you’re solving for
- Use one step per line
- Keep variables in alphabetical order when possible
- Practice rewriting formulas in different ways
It also helps to talk through your steps out loud. Believe it or not, hearing your logic often catches small mistakes early.
Literal Equations in Science and Real Life
Literal equations aren’t just classroom tools—they explain the world around us.
They appear in:
- Physics formulas like force and velocity
- Chemistry equations for concentration
- Geometry rules for shapes
- Finance formulas for interest
- Engineering designs and calculations
Whenever a formula has letters instead of numbers, you’re looking at a literal equation in action.
That’s why learning them well opens doors far beyond math class.
Practice Makes Progress with Literal Equations
There’s no shortcut here—practice really does make a difference. The more literal equations you work through, the more natural they feel.
Start with simple formulas. Then gradually move to more complex ones. Over time, you’ll notice patterns, and solving becomes faster and smoother.
Remember, every expert was once a beginner who kept practicing.
Building Confidence and Trust in Your Math Skills
Literal equations often feel difficult because they require flexible thinking. You’re not following a single formula—you’re reshaping one.
That’s a powerful skill.
With consistent practice, literal equations stop feeling like puzzles and start feeling like tools. And once that happens, algebra becomes less stressful and far more rewarding.
Final Thoughts on Literal Equations
Literal equations are a cornerstone of algebra and a gateway to higher-level thinking. They teach logic, balance, and problem-solving in a way few other math topics can.
By understanding how literal equations work, practicing carefully, and applying smart strategies, students can master this topic with confidence. These skills don’t just help in math—they build a mindset that supports learning across all subjects.
Whether you’re a student, teacher, or lifelong learner, mastering literal equations is a step forward—and one that truly pays off.